线性回归问题最常见的两个方法,一个是最小二乘法,另一个就是梯度下降. 上一章我们说明了梯度下降法的原理。现在我们就来看一下线性回归到底是什么类型的问题,以及梯度下降法在线性回归中的实际应用。
线性回归 Linear regression
定义 Definition
看一下线性回归的定义:
Linear regression is a linear model, e.g. a model that assumes a linear relationship between
the input variables (x) and the single output variable (y).
More specifically, that output variable (y) can be calculated from a linear combination of
the input variables (x).Linear Regression on Wikipedia
特征 Features
每一份训练的样本中都包含了用于描述样本的特征,也就是变量。
n 表示特征数
Rn+1 表示包含n+1个实数的向量
对于单变量的线性回归,特征数n是1,只有x0一个特征
参数 Parameters
对于这些特征xi而言,每个特征都有一个参数值θi
假设 Hypothesis
线性回归问题基于的假设就是,输出值y与X是存在线性关系的。也就可以用下面的表达式进行定义
其中θi是参数,也就是我们希望模型能够计算出的结果。为了方便标记,我们将x0定义为1
价值函数 Cost Function
线型回归问题终究是基于线性关系的假设,那如何衡量我们计算出的θ的准确性呢?那显然需要用到cost function(价值函数)。也可以称作误差方程,损失函数等等。
xi - 第i个样本的特征值
yi - 第i个样本的输出值
m - 样本个数
在线性回归中,损失函数通常为样本输出和假设函数的差取平方。这里就是采用这种方式。
线性回归中的梯度下降
代数表示方法
样本
首先我们有n个样本数据
也可以表示为:

价值函数求梯度
接着我们对价值函数(误差方程)求偏导:

确定参数的初始值
例如我们可以初始化都赋值成1
生成参数的转移矢量
根据学习速率确定步长α,乘以损失函数的梯度,这样我们就能得到参数的转移矢量,模就是θ的梯度下降距离
生成新参数
参数的转移矢量的大小,如果所有的θ的梯度下降距离都小于阈值ε,那么计算终止。如果不满足要求,那么
矩阵表示
样本
样本可以用矩阵X Y表示。
假设函数
θ表示n1的参数矩阵,*X**表示nx1的自变量矩阵
价值函数
价值函数的定义也用矩阵形式表示:
价值函数的梯度
确定参数的初始值
这里我们同样把参数初始化都赋值成1
生成参数的转移矢量
生成新参数
参数的转移矢量的大小,如果所有的θ的梯度下降距离都小于阈值ε,那么计算终止。如果不满足要求,那么
过拟合及解决方案 Overfitting and Solution
过拟合 Overfitting
什么是过拟合?简单来说就是机器学习模型过于执着于完美。我们知道实际中的数据肯定是包含随机误差的,以线性回归问题为例,我们训练器学习模型,去找到一条符合我们要求的回归方程即可。而数据点由于包含误差,或者本身回归方程本身也只是近似解,势必会有一些点不落在回归方程上。过拟合又是什么呢?就是为了让结果尽可能的好看(误差方程的值尽可能的小),而推算出极其复杂的模型,违背了我们寻求简单近似回归方程的本意。
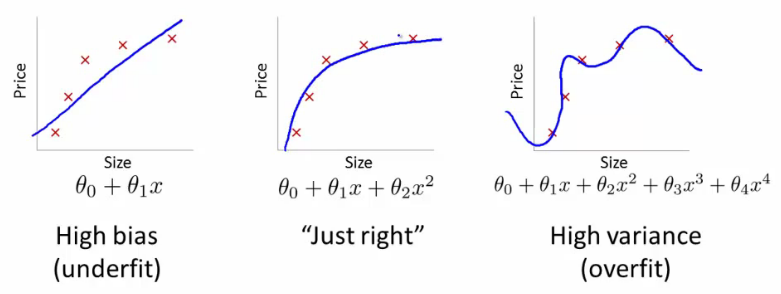
其它问题例如分类问题,也会有过拟合的问题。

解决方案 Solution
一个解决思路是提高样本量。小样本下个例容易被当做普通情况,而样本量足够大的话,会减少机器学习模型过拟合的问题。
正规化 Regularization
另一个解决办法是正规化。在下图中,蓝色的线代表的方程虽然误差较红色的大,但显然是更优于红色的线的。
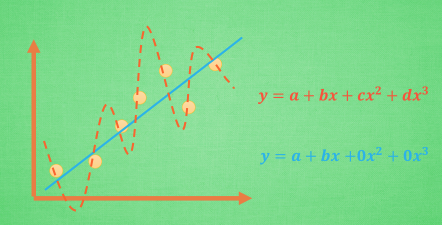
正规化的解决思路就是让红色的回归方程在增加参数导致复杂化的时候,付出相应的代价。换句话说,我们对误差方程中,参数的复杂程度也做为一个评判标准,太复杂的结果误差就大,这样就可以避免过拟合的问题。

如上图所示,我们在误差方程的后面加上只跟参数相关的部分,平方和的正规化称为L2正规化,绝对值的和称为L1正规化。
具体可以参考:
莫凡 有趣的机器学习 L1 / L2 正规化 (Regularization)
线性回归的正规化
这里假设我们采用L2正规化的方法,更新我们的误差方程:
λ是正规化参数,值得注意的是,对于θ0,也就是参数项,我们不应该去正规化它。
这样的话,第四步的计算公式更新为:

















