上一章我们使用TensorFlow搭建了一个非常简单的关于单参数线性回归的神经网络,并取得了非常好的运行效果。在分析线性回归前,我们有必要针对梯度下降法做一个介绍,看看梯度下降法到底是怎么一回事?
基础 Basic
多元函数
首先引出多元函数的概念。在实际问题中尝尝要研究多个变量之间的关系。线性回归问题中同样如此,上一章y关于x的线性回归方程显然只有x一个变量,也就是一元函数。而真实情况下,变量的数目远远不止一个。
方向倒数和偏导数
对于一元函数而言,x0点导数也就是该点切线的斜率。
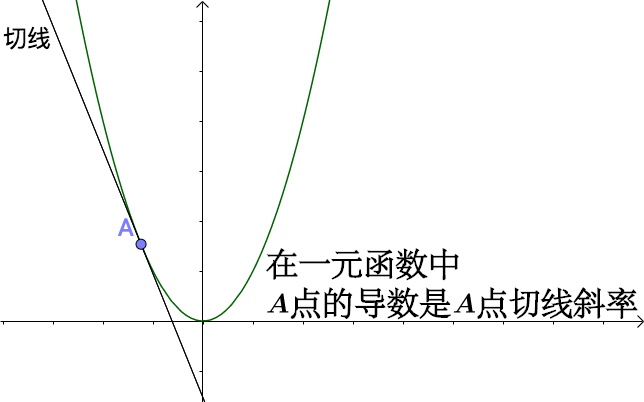
导数的定义是
而由单侧极限引申出单侧导数,也就是左导数,右导数
对于多元函数而言,任意一个点的导数可能有无数个。想象一个漏斗曲面上任意一点,经过该点我们显然可以沿着不同的方向做无数条切线,而这些切线的斜率都是该点的导数。也就是全导数。
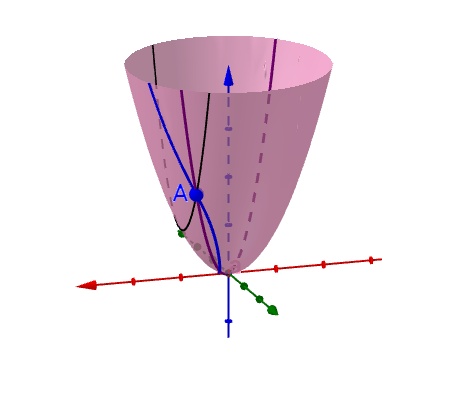
而这些不同方向的导数我们称之为方向导数
其中l是方向向量,el是l方向上的单位方向向量。
方向导数实际上是函数f在x<sup>0</sup>处沿l方向关于距离的变化率。偏导数又是什么概念呢,其实就是对函数中某个变量求导数。例如二元函数f(x,y)在(x0, y0)点假设可导,那么它的方向导数当中,x轴正方向导数,x轴负方向导数,y轴正方向导数,y轴负方向导数都是它的偏导数。
梯度
梯度:是一个矢量,其方向上的方向导数最大,其大小正好是此最大方向导数。从直观的角度来说,以爬山为例,三维空间我们建立起高度(z)关于经纬度(x, y)的二元函数。所谓的梯度也就是,当你站在山的任意一个位置时,想爬山的你其实有无数个方向可以选择。而上山角度最陡峭,也就是爬山最快的那个方向,就是梯度得方向,而这个方向的导数的值,也就是梯度的模。没错,梯度是个矢量,有大小和方向。
从数学角度,函数
的如果在点x0处可微,那么f在x0的梯度就是这个点的偏导数,记作grad f(x0) 或 ∇ f(x0)
[如何直观形象的理解方向导数与梯度以及它们之间的关系? - 马同学的回答 - 知乎]
(https://www.zhihu.com/question/36301367/answer/156102040)
梯度下降 Gradient Descent
一元函数的梯度下降
我们总算了解了梯度的概念。那么梯度下降到底是个什么样的方法呢?
简而言之就是沿着梯度的方向,尝试找到误差方程的最小值。
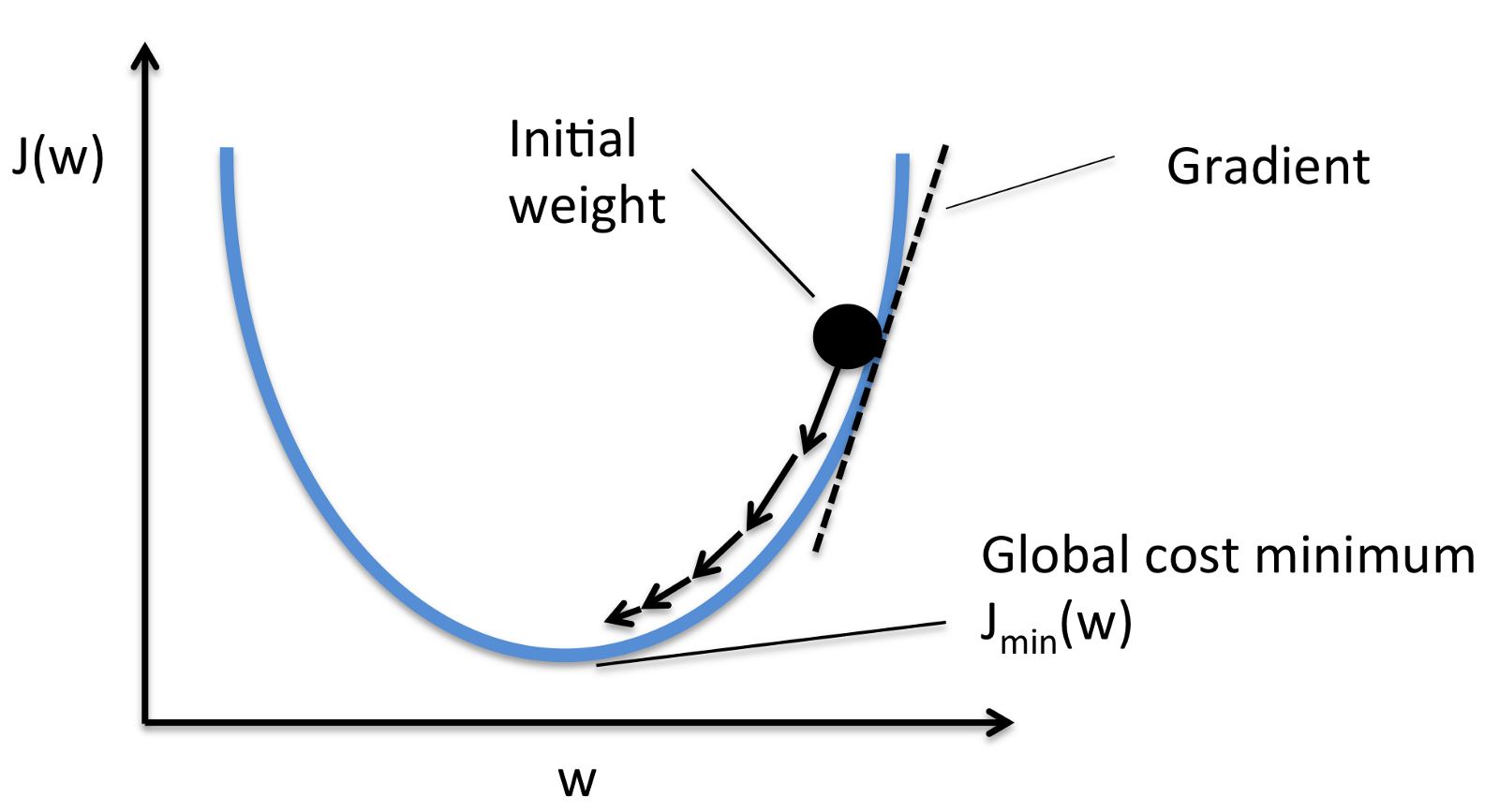
什么意思?还是以最简单的一元函数为例,假设图中的曲线是我们的误差方程曲线,小球的位置就是我们随机给的初始值。根据这个初始值,我们能得到误差方程的初始函数值。我们接下来尝试沿着该点的梯度的方向,去移动这个初始点。(为什么是梯度而不是其他的方向导数,因为梯度其方向上的方向导数最大,也就是最快,有捷径我们自然不会去绕远路)。如此反复之后,直到我们获得的误差方程的的值小于我能接受的范围,那么最终小球的位置就是我们要找的值。

这里很显然带来了两个问题。
- 我找到的点,就一定是最低点吗?也就是说,我找到的点,就一定是误差方程的最小值点吗?
- 梯度的方向有了,那小球每次移动的距离是多少?
第一个问题显然,我们无法保证找到的点就一定是最值点。根据误差方程,初始位置,甚至是步长的不同,我们很可能找到的是一个极值点。形象点说,下山的时候,你走了一段路,发现来到了一处谷底,这个谷底一定是山脚吗?不一定,它也可能只是山上的一处低处。当然,图中实例的曲线,显然是一个凸函数,那我们找到的极值点也一定是它的最值点。
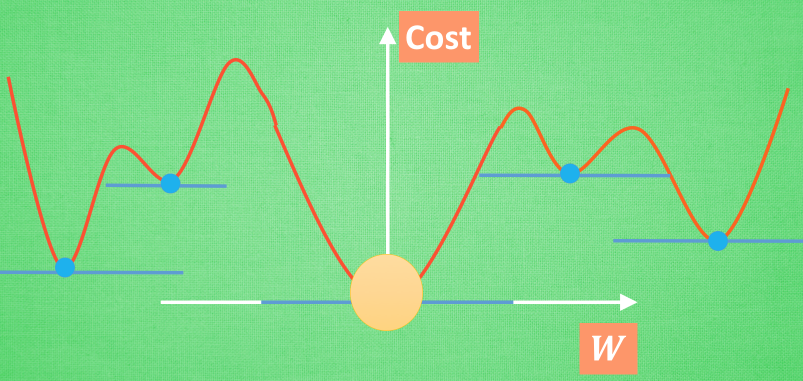
第二个问题,也就是步长的问题,这个和初始点的位置一样,我们可以手动去设置它的值,也就是学习速率。如下图所示,学习速率太小可能导致计算次数变多,时间变得很长。而学习速率过大,则很可能导致一直在极值点附近跳跃,到达不了理想的位置。所以,合理的学习速率非常重要。

多元函数的梯度下降及算法
二元函数的梯度下降也可以直观的描述。看下图就好,这里就不多说了。
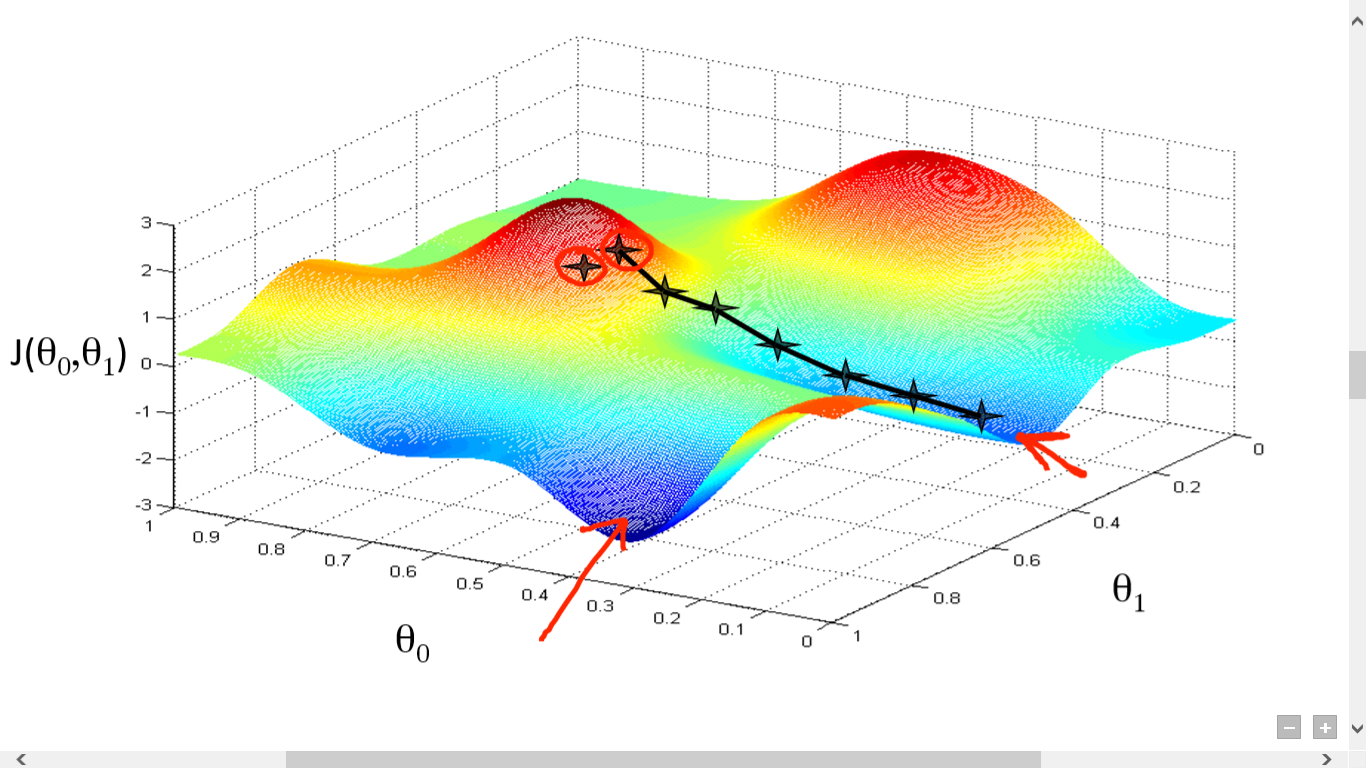
同理多元函数的梯度下降也是类似的,这里就不赘述了。





