回归问题，尤其是单变量的线性回归问题，一般是机器学习中入门时最常举的例子。我们也不例外，就从线性回归问题聊起。我们上篇先看一个简单的实现例子，下篇我们再聊涉及理论的方面。

例子

为了避免一开始就丟公式和原理，我们先看代码，有个感性上的认识。这里我们以『单变量的线性回归』为例.

库的导入

首先是导入相关库

1 2	import tensorflow as tf import numpy as np

生成随机数据

接着是原始数据，这里我们通过numpy的随机函数，创建100个(x, y)的点，满足 y = 0.1x + 0.3

1 2	x_data = np.random.rand(100).astype(np.float32) y_data = x_data * 0.1 + 0.3

这里因为是我们自己生成的数据，我们自然知道可以用线性回归去拟合这些点。
同时数据样本的值比较小，数据标准化的步骤我们也省略。下面直接开始搭建深度学习网络。

构建张量

网络搭建的第一步，我们需要去定义出我们通过深度学习网络，到底要计算出什么样的结果。很显然，假如我只知道我的数据大致符合：

y = w*x+b

这样的线型方程。那么，我希望深度学习网络能顺利的输出w和b的值，接近我预设的真实值。

1 2	weights = tf.Variable(tf.random_uniform([1], -1.0, 1.0)) biases = tf.Variable(tf.zeros([1]))

只要你看了上一章TensorFlow入门2-基础概念, 对这里张量的定义肯定不会太陌生。为了更直观的了解到我们这两行到底做了什么，我们可以拆开了这样写：

weights_initial_value = tf.random_uniform(shape=[1], minval=-1.0, maxval=1.0)
weights = tf.Variable(initial_value=weights_initial_value)
biases_initial_value = tf.zeros(shape=[1])
biases = tf.Variable(initial_value=biases_initial_value)

定义张量y，也就是我们的预测值。

1 2	# 张量支持四则运算 y = weights * x_data + biases

到这一步，我们定义了三个张量，weights和biases分别对应着公式中的w和b，而y是预测值。我们可以打印出这三个张量：

1
2
3

<tf.Variable 'Variable:0' shape=(1,) dtype=float32_ref> 
<tf.Variable 'Variable_1:0' shape=(1,) dtype=float32_ref> 
Tensor("add:0", shape=(100,), dtype=float32)

定义损失函数和优化器

接下来我们需要定义的是损失函数和优化器。前者是我们评价预测结果好坏的计算方法，后者则是深度学习网络根据预测值进行迭代优化的真正的方法。这里我们选用的是梯度下降法。

# 输入张量是预测值和实际值的平方差，实际损失是通过tf.math.reduce_mean方法定义的求均值的算术操作
loss = tf.math.reduce_mean(input_tensor=tf.square(y - y_data))
# 定义梯度下降作为优化器,学习速率是0.5
optimizer = tf.train.GradientDescentOptimizer(0.5)
# 定义实际操作就是使用梯度下降优化器去最小化损失函数
train = optimizer.minimize(loss)

创建会话并运行

到了真正开始执行运算的一步了。

# 记得初始化变量
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

for step in range(201):
    sess.run(train)
    if step % 20 == 0:
        print(step, sess.run(weights), sess.run(biases))

输出结果

[0.4496472] [0.]
0 [0.4820045] [0.12873188]
20 [0.18697067] [0.25420249]
40 [0.12046056] [0.28922576]
60 [0.10481351] [0.2974653]
80 [0.10113242] [0.2994037]
100 [0.1002664] [0.29985973]
120 [0.10006267] [0.29996702]
140 [0.10001475] [0.29999223]
160 [0.10000348] [0.2999982]
180 [0.10000083] [0.29999956]
200 [0.1000002] [0.29999992]

可以看到，深度学习网络，通过梯度下降方法，经过201次的训练，已经可以很精确的算出w和b的值。

完整代码

import tensorflow as tf
import numpy as np

# create data
x_data = np.random.rand(100).astype(np.float32)
y_data = x_data * 0.1 + 0.3

weights = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
biases = tf.Variable(tf.zeros([1]))
y = weights * x_data + biases

loss = tf.math.reduce_mean(tf.square(y - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

for step in range(201):
    sess.run(train)
    if step % 20 == 0:
        print(step, sess.run(weights), sess.run(biases))

可视化

数据增加噪音

通常情况下，我们的数据不会像我们之前展示的那样的完美，所以我们有必要给数据增加上噪音偏差，让它不会恰好完美的落在一条直线上。

1
2
3

x_data = np.random.rand(100).astype(np.float32)
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)
y_data = x_data * 0.5 + 0.3 + noise

可视化原始数据

import matplotlib.pyplot as plt

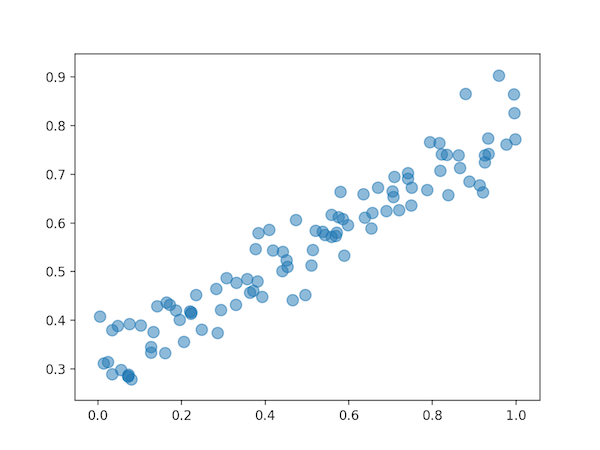
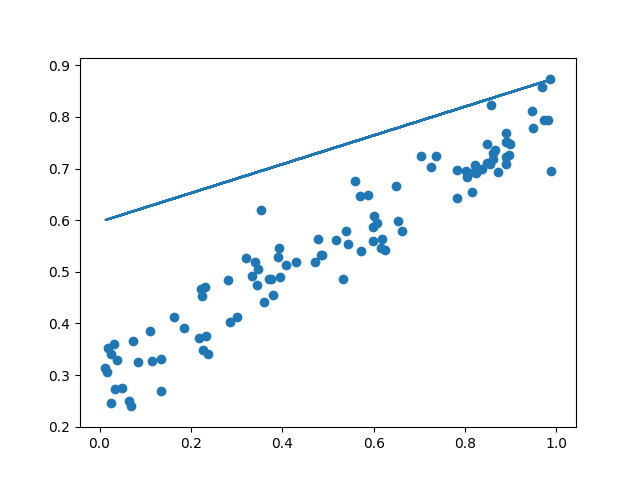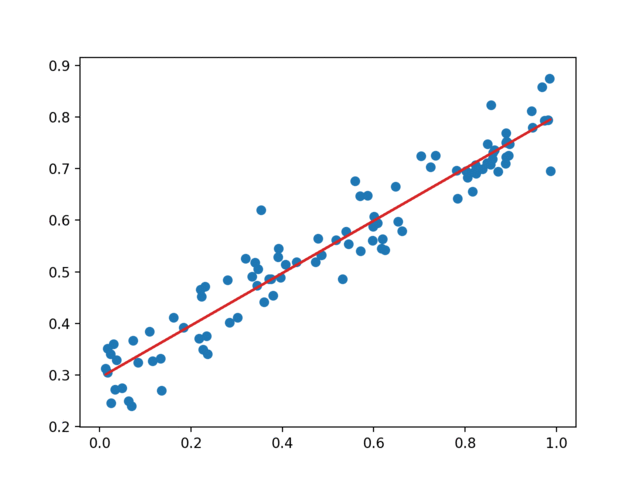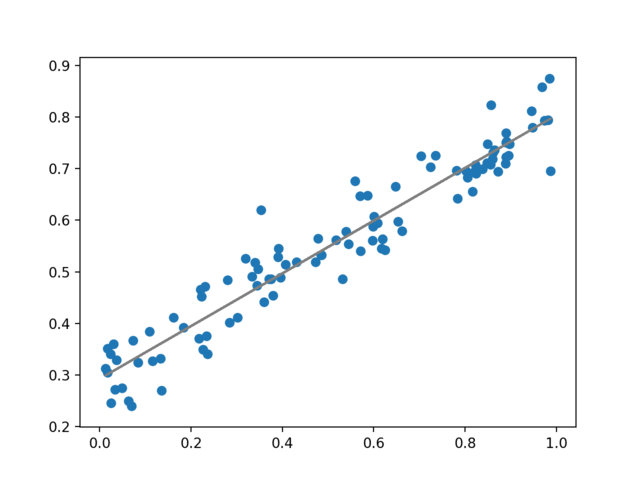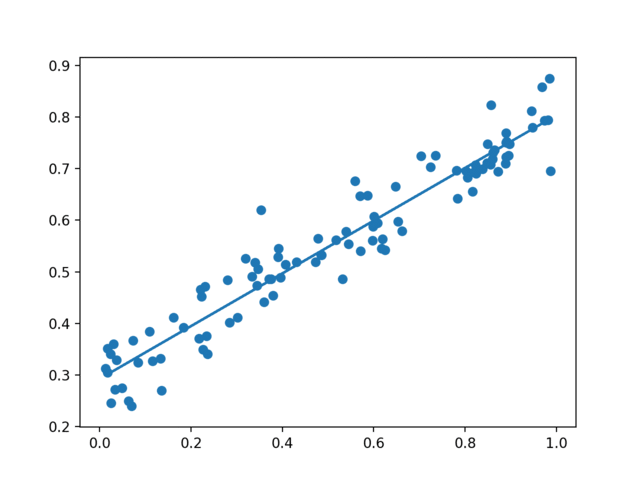
plt.scatter(x_data, y_data, s=75, alpha=0.5)
plt.show()

让我们给图加一个y=0.5x+0.3的线段

1
2
3

x = np.linspace(0, 1, 10)
y = x * 0.5 + 0.3
plt.plot(x, y, label='linear')

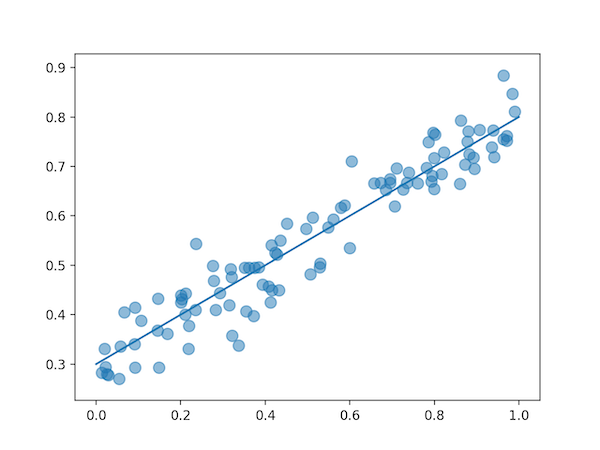
可视化结果

同样的，我们可以动态的展示深度学习网络计算出的结果

for step in range(201):
    sess.run(train)
    if step % 20 == 0:
        weights_value = sess.run(weights)
        biases_value = sess.run(biases)
        print(step, weights_value, biases_value)
        if 'lines' in locals().keys():
            # 移除上一次画的拟合线
            ax.lines.remove(lines[0])
        lines = ax.plot(x_data, weights_value * x_data + biases_value)
        plt.pause(1)