TensorFlow入门2-基础概念

发表于 | 分类于

接触TensorFlow之前，有必要了解一下TensorFlow当中的基础概念。这里简单梳理下TensorFlow的数据流图, 张量, 会话, 优化器等概念。

本文内容已于2019年09月10日，Google开发者大会当日更新。

TensorFlow是什么

TensorFlow是Google推出的开发和训练机器学习模型的核心开源库。

TensorFlow官网

TensorFlow仓库地址

TensorFlow Python API

目前TensorFlow已经发布了2.0 RC版，对于目前大面积使用的1.x的接口有了相当程度的改动。本文我们还是以1.x的API为例。

TensorFlow 模块与Api

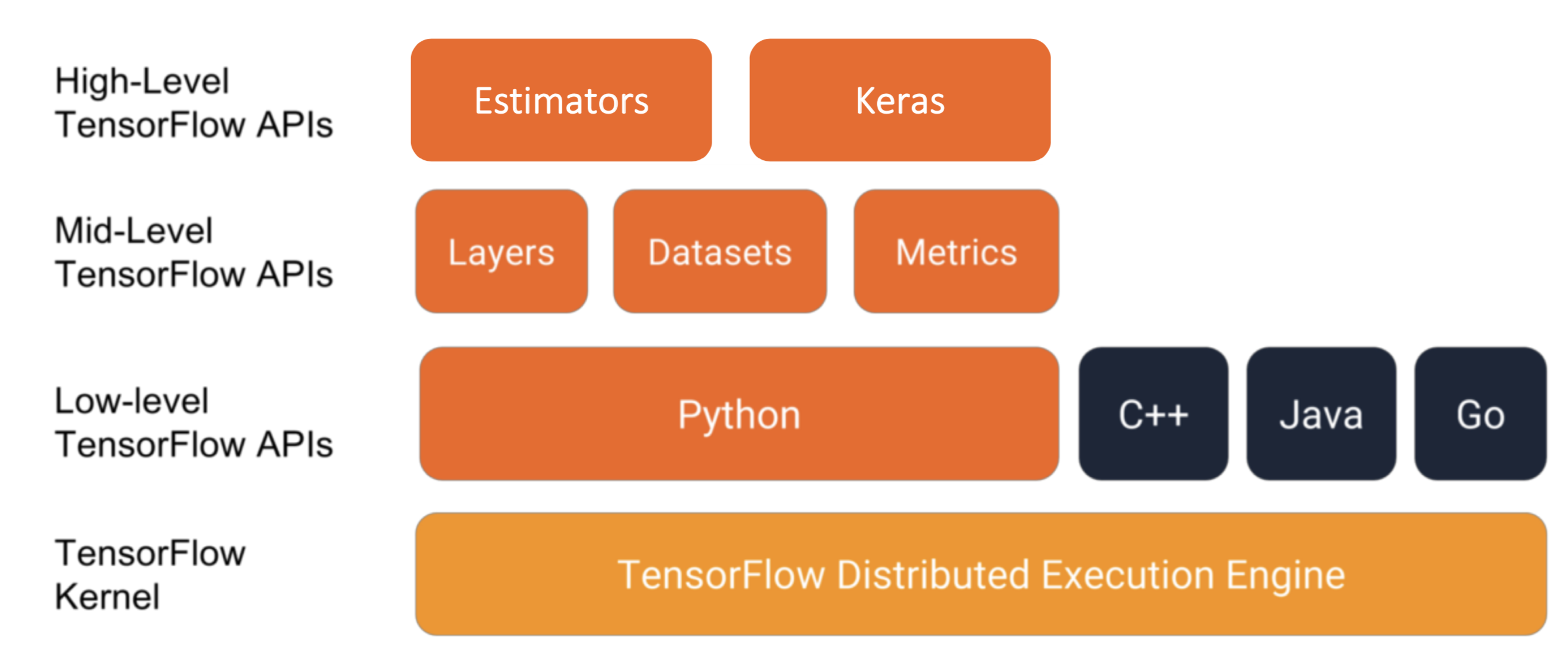
从这张图中我们看到，TensorFlow设计了高中低不同等级的API，并且多语言的兼容性使得开发者可以尽可能的使用自己熟悉的开发语言。

TensorFlow 架构

数据流图 Dataflow graph

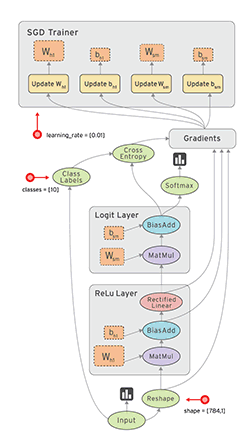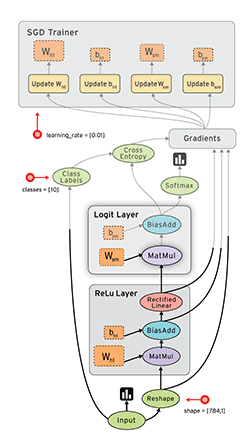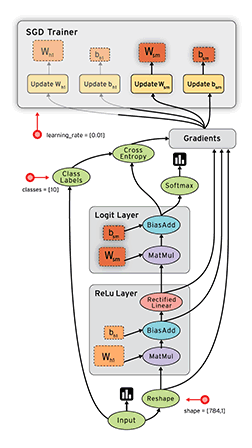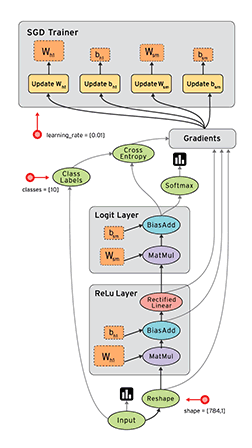
这张官网的动图就很直观的表现了TensorFlow是如何构建算法模型的。这里我们不仔细展开，但是也可以发现，动图中表示的是，数据以流的形式在一张包含特定结构的图中进行流动。具体来说：

TensorFlow用数据流图表示算法模型。

为什么使用数据流图？

TensorFlow数据流图是一种申明式的编程规范。

这里不展开说哈，像Lambda表达式其实就是一种申明式，或者说函数式的编程。

具体到数据流图，它是由节点和有向边组成, 下面有一张结构图：

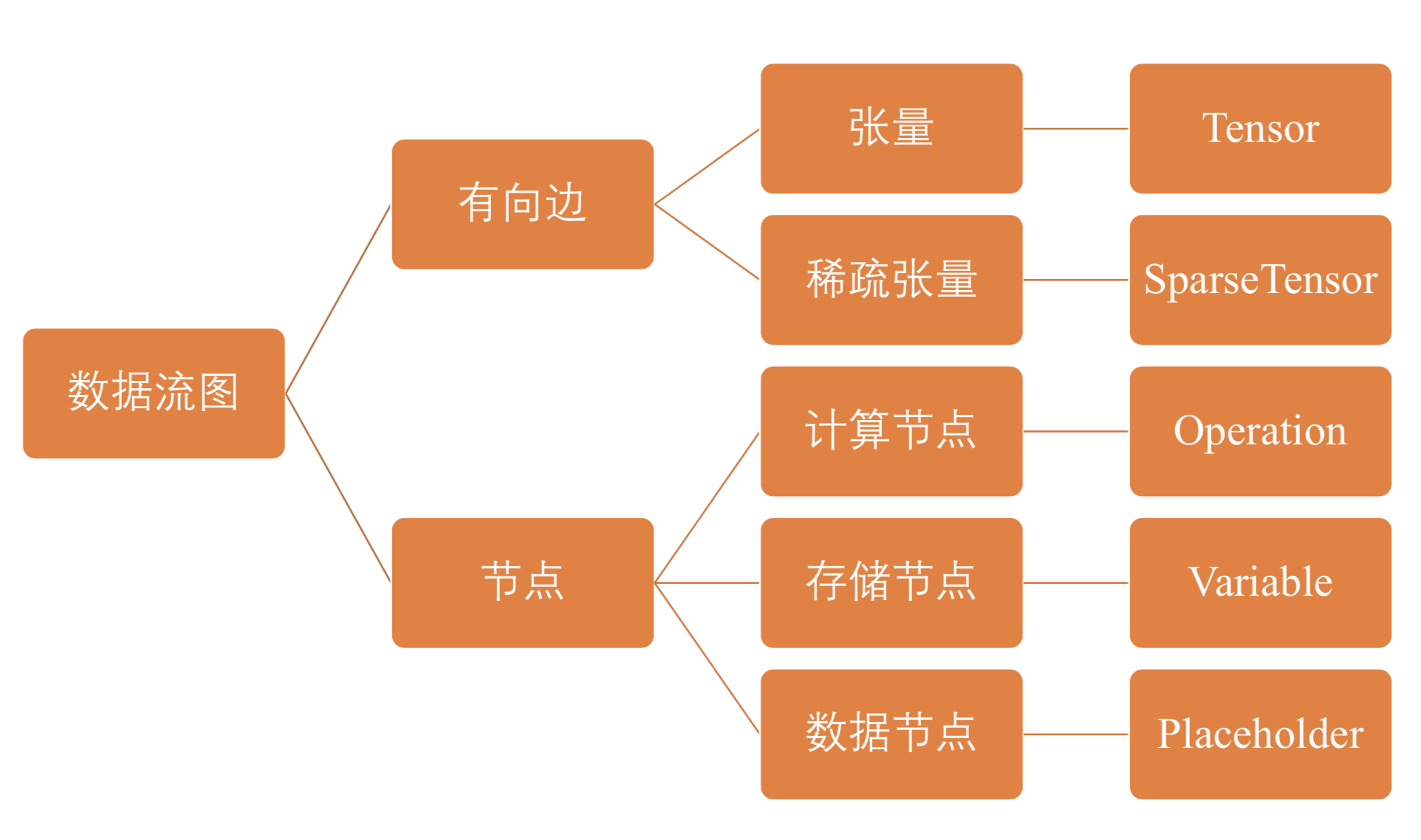
操作

数据流图中的每个节点对应一个具体的操作。因此，操作是模型功能的实际载体。
也就是说，

节点分为三类：

存储节点(Variable) 有状态的变量参数,通常用来存储模型参数
计算节点(Operation) 无状态的计算或控制操作，主要负责算法逻辑表达或流程控制
数据节点(PlaceHolder) 数据的占位符操作,用于描述图外输入数据的属性

用比较专业的术语来概括下数据流图：

TensorFlow数据流图描述了算法模型的计算拓扑，其中各个操作(节点)都是抽象的函映射或数学表达式。
换句话说，数据流图本身是一个具有计算拓扑或内部结构的『壳』,在用户向数据流图填充数据前，图中并没有执行任何计算。

从图论的角度，TensorFlow中的图，是一个有向无环图。

张量 Tensor

张量 Tensor 和 稀疏张量 Sparse Tensor

官网对张量的解释：

正如名称所示，TensorFlow 这一框架定义和运行涉及张量的计算。张量是对矢量和矩阵向潜在的更高维度的泛化。
TensorFlow 在内部将张量表示为基本数据类型的 n 维数组。

简单来说呢，张量表示某种相同类型的多维数组

在TensorFlow中，张量具有有数据类型和形状两个基本属性。

  • 数据类型(如浮点型，整型，字符串)
  • 数组形状(各个维度的大小)

而相对着稀疏张量 SparseTensor 维度很高，但是数据量稀疏。熟悉线性代数的同学应该知道稀疏矩阵的概念，稀疏张量类似，通过在存储上只存形状和有意义的数值，可以大幅的减少存储空间以及计算量。

所以，总结一下TensorFlow 张量是什么？

  • 张量是用来表示多维数组的
  • 张量是执行操作时的输入或输出数据
  • 用户通过执行操作来创建或计算张量
  • 张量的形状不一定在编译时确定，可以在运行时通过形状推断计算得出

阶 Rank

tf.Tensor的阶也就是它的维度数。阶的同义词包括：秩（order）、等级（degree）或 n 维（n-dimension）

阶 数学实例
0 标量（只有大小）
1 矢量（大小和方向）
2 矩阵（数据表）
3 3 阶张量（数据立体）
4 n 阶张量（自行想象）

总结起来，张量就是TensorFlow里的数据单元。根据阶数不同，有0阶的就是一个数字。一阶的向量，二阶的矩阵等等。

实践

先介绍几类特殊的张量

tf.constant //常量
tf.placeholder //占位符
tf.Variable //变量

常量很好理解，就是创建后无法修改值的张量。
占位符可以理解为初期不赋值，等到程序实际运行起来，才输入具体值的张量。
而通过tf.Variable创建的变量，和普通的张量相比，区别在于

  • 张量的生命周期通常随依赖的计算完成而结束,内存也随之释放
  • 变量则常驻内存，在每一步计算时不断更新其值, 以实现模型参数的更新。

相对来说，变量可以用于维护特定节点的状态,如深度学习或机器学习的模型参数

  • 首先是导入相关库
1
import tensorflow as tf
  • tf.constant可以定义常量张量, tf.Variable可以定义变量张量
1
2
3
4
5
6
7
8
9
10
11
# 定义阶为0，数据类型为float, 名称为aaa的常量张量，初始值为1
variable1 = tf.constant(value=1, dtype=float, shape=[], name='aaa')
# Tensor("aaa:0", shape=(), dtype=float32)

# 定义阶为0，数据类型为float, 名称为bbb的变量张量，初始值为1
variable2 = tf.Variable(initial_value=1, dtype=float, name='bbb')
# <tf.Variable 'bbb:0' shape=() dtype=float32_ref>

# 定义阶为1(形状为(1, ))，数据类型为float, 名称为ccc的变量张量，初始值为[1,1]
variable3 = tf.Variable(initial_value=[1, 1], dtype=float, name='ccc')
# <tf.Variable 'ccc:0' shape=(2,) dtype=float32_ref>

另外还有一些常用的定义张量的方法，如tf.placeholder定义占位符张量(初始不赋值，运行时才赋值),tf.random_uniform生成随机值张量，tf.zeros定义全零张量等等。

细心的朋友可能会发现，这里输出的张量信息当中并没有初始化的值信息。那么如何才能打印出张量的值呢？

会话 Session

绘画提供了估算张量和执行操作的运行环境,它是发放计算任务的客户端,所有计算任务都由他连接的执行引擎完成。

会话允许你执行图或者图的一部分。它为图分配资源(一台或多台机器)，并且保存中间结果和变量的实际值。

说了一堆概念，下面我们来看看如何创建会话，并在会话中执行一些简单操作：

创建会话有两种方式

1
2
3
4
5
6
7
8
9
10
# 1. 创建会话
# target 会话连接的执行引擎, graph 会话加载的数据流图, config 会话启动的配置项
sess = tf.Session(target=...,graph=...,config=...)
# 2. 估算张量或执行操作
sess.run(...)
# 3. 关闭会话
sess.close()

with tf.Session() as sess:
  sess.run(...)

例如我想打印前面的几个张量的值，那么我可以这样写：

1
2
3
4
5
with tf.Session() as sess:
    print(sess.run(variable1))  #1.0
    # 下面两行报错 tensorflow.python.framework.errors_impl.FailedPreconditionError: Attempting to use uninitialized value bbb
    #print(sess.run(variable2))  
    #print(sess.run(variable3))

这里我们需要注意，在图中使用变量张量的时候，需要调用初始化方法：

1
2
3
4
5
6
init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    print(sess.run(variable1))  #1.0
    print(sess.run(variable2))  #1.0
    print(sess.run(variable3))  #[1. 1.]

获取张量值的另外两种方法：估算张量(Tensor.val)和执行操作(Operation.run)，这两个方法最终也在内部调用了session.run()方法

优化器 Optimizer

在了解优化器之前，需要了解关于损失函数和优化算法的知识。

损失函数

损失函数是用来评估特定的模型参数和特定输入时,表达模型输出的推理值和真实值的不一致程度的函数。损失函数L的形式化定义是：

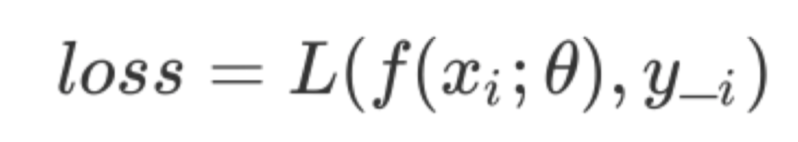
我们知道，训练模型的最终目的是能够合理的降低损失函数的值，这里可能会存在过拟合的问题，就不展开细说了。

优化算法

典型的机器学习和深度学习问题通常都需要转换为最优化问题进行求解。而求解最优化问题的算法成为优化算法。他们通常采用迭代方式进行。首先设定一个初始的可行解，然后基于特定的函数反复重新计算可行解,直到找到一个最优解或者达到预设的收敛条件。不同优化算法采用的迭代策略不同：

  • 有的使用目标函数的一阶导数，如梯度下降法
  • 有的使用目标函数的二阶导数，如牛顿法
  • 有的使用前几轮的迭代信息，如Adam

简单来说,典型的机器学习和深度学习问题,包含模型定义，损失函数定义，优化算法定义三个部分

优化器

优化器是优化算法的载体,一次典型的迭代优化应该分为以下三步：

  1. 计算梯度,调用compute_gradients()方法
  2. 处理梯度 用户按照自己需求，处理梯度值,如梯度裁剪和梯度加权
  3. 应用梯度: 调用apply_gradients方法,将处理后的梯度值应用到模型参数。